Let a and b be equal non-zero quantities
Multiply through by a
Subtract 
Factor both sides
Divide out 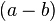
Observing that 
Combine like terms on the left
Divide by the non-zero b
The fallacy is in line 5: the progression from line 4 to line 5 involves division by (a − b), which is zero since a equals b. Since division by zero is undefined, the argument is invalid. Deriving that the only possible solution for lines 5, 6, and 7, namely that a = b = 0, this flaw is evident again in line 7, where one must divide by b (0) in order to produce the fallacy (not to mention that the only possible solution denies the original premise that a and b are nonzero). A similar invalid proof would be to say that 2(0) = 1(0) (which is true) therefore, by dividing by zero, 2 = 1.
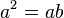



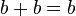

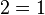
No comments:
Post a Comment